../

HeroCTF v6 - Interpolation [crypto]

HeroCTF v6 writeup for interpolation challenge

Difficulty : Easy

Team : Langskip

Source files

Has missing data really stopped anyone ?

Author : alol

TL;DR

  • Get the computed points that the server send us
  • Compute f(0) with the by knowing that Hero is used to generate the first coefficient a0
  • Interpolate with the points we have
  • Compute every flag part by using a rainbow table

Introduction

We have a server that creates a polynomial from the flag which is cut into several parts and then hashed.

It calculates points with this polynomial and sends them to us.

Solving

Reading the challenge source code

chall.sage 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

#!/usr/bin/sage
import hashlib
import re

with open("flag.txt", "rb") as f:
    FLAG = f.read()
    assert re.match(rb"Hero{[0-9a-zA-Z_]{90}}", FLAG)

F = FiniteField(2**256 - 189)
R = PolynomialRing(F, "x")
H = lambda n: int(hashlib.sha256(n).hexdigest(), 16)
C = lambda x: [H(x[i : i + 4]) for i in range(0, len(FLAG), 4)]

f = R(C(FLAG))

points = []
for _ in range(f.degree()):
    r = F.random_element()
    points.append([r, f(r)])
print(points)

flag = input(">").encode().ljust(len(FLAG))

g = R(C(flag))

for p in points:
    if g(p[0]) != p[1]:
        print("Wrong flag!")
        break
else:
    print("Congrats!")

  • Here : assert re.match(rb "Hero{[0-9a-zA-Z_]{90}}", FLAG), we know the characters used for the flag, their number of 90, and added to this Hero{}, the flag has a length of 96 characters.

  • A finite field is defined: F = FiniteField(2**256 - 189) also noted $ \mathbb{Z}/n\mathbb{Z} $ with $ n = 2^{256} -189 $. This is a notion of modular arithmetic which implies that all the numbers we work with are modulo n. There’s a cryptohack module that covers these notions.

  • Next, we initialize a polynomial object in the finite field F: R = PolynomialRing(F, "x"). It is polynomial with one variable x, so we call it a univariate polynomial.

  • A H function that only hashes given bytes and the C function slices a string into 4-byte chunks, hash each of them with H and add them to a list.

1
2

H = lambda n: int(hashlib.sha256(n).hexdigest(), 16)
C = lambda x: [H(x[i : i + 4]) for i in range(0, len(FLAG), 4)]
  • Then the polynomial is generated with: f = R(C(FLAG)).

By the way, a polynomial P is written:


$$ P(X) = a_{n}X^{n} + a_{n-1}X^{n-1} + ... \ + a_{2}X^{2} + a_{1}X^{1} + a_{0} $$

Basically, the quadratic equation we saw in high school was a polynomial:


$$ ax^{2} + bx +c $$

It’s called a second degree polynomial equation, because the degree of a polynomial is the largest integer i such that $ a_{i} \neq 0 $.

And the coefficients are the values a of the polynomial P.

  • There are n random numbers x generated, their y image is calculated through the polynomial and the [x,y] pair is added to the points list. And this list of points is sent to us.
1
2
3
4
5

points = []
for _ in range(f.degree()):
    r = F.random_element()
    points.append([r, f(r)])
print(points)
  • Then a user input is requested, and a polynomial will be generated as it was with the FLAG and the results obtained with our input will be compared with the results obtained with the polynomial generated with the FLAG.
1
2
3
4
5
6
7
8

g = R(C(flag))

for p in points:
    if g(p[0]) != p[1]:
        print("Wrong flag!")
        break
else:
    print("Congrats!")

The FLAG will not be displayed at the end of our user input, so we should be able to find the flag on our side.

Vulnerabilities

The logical path for me is that, from the points and their images sent by the server, reconstruct the original polynomial.

Recover the coefficients of the polynomial and then trace back to the value of each coefficients before being hashed.

It’s a kind of bruteforce and I’m going to use a rainbow table for this.

Polynomial recovery

A polynomial can be reconstructed if we have enough of its points and images with the lagrange interpolating polynomial. This is the concept behind Shamir’s secret key sharing.

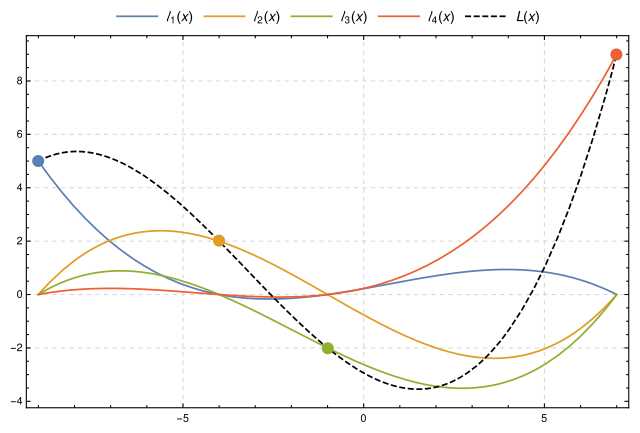
lagrange polynomial

For the theory, we’ll draw a curve that passes through a point thanks to an equation, reproduce this for all the submitted points and multiply all the equations, here’s what the final equation looks like:

$$ l_{i}(X) = \prod_{j=0,j\neq i}^{n} \frac{X - x_{j}}{x_{i} - x_{j}} \ ... \ \frac{X - x_{0}}{x_{i} - x_{0}} \frac{X - x_{1}}{x_{i} - x_{1}} \ ... \ \frac{X - x_{n}}{x_{i} - x_{n}} $$

The server sends us 23 points and we can try to reconstruct the polynomial with them:

trying to recover the polynomial 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

from pwn import remote

host = 'crypto.heroctf.fr'
port = 9000

conn = remote(host, port)

data = conn.recvuntilS('>').decode()
given_points = eval(data.split('\n')[0])

F = FiniteField(2**256 - 189)
R = PolynomialRing(F, "x")

interp = R.lagrange_polynomial(given_points)
coefs = interp.coefficients()

print(coefs)
print(interp)

spoiler: we get the wrong polynomial.

I tested locally with a flag of the same format as the flag used in the challenge. I generated the polynomial from the flag and another polynomial by interpolation and they don’t match.

The explanation is that I’m not generating the polynomial with enough points. I’m using 23, which generates 23 coefficients, whereas the original polynomial has 24 (to calculate this, just calculate the length of the list generated by C(FLAG)). However, I can calculate one more.

When the polynomial is generated with f = R(C(FLAG)), a list of int is generated with C(FLAG). The polynomial is then generated from this list. Except that the first element of the list will be converted to a coefficient with x to the power 0: $ a_{0}X^{0} = a_{0} $. In other words, points[0] becomes $ a_{0}X $ and points[1]` becomes $ a_{1}X^{1} $ …

For example, with a list of points: [7, 4 ,3] we’ll have this polynomial: $ 3X^{2} + 4X^{1} + 7 $. And so, calculating the polynomial for x = 0 is like 3*0 + 4*0 + 7 = 7.

It turns out that the first coefficient is generated with the first four characters of the flag : Hero and will represent the variable $ a_{0} $. So calculating $ f(0) $ gives $ a_{0} $.

So we computes a0 :

1
2
3
4
5
6
7

from sage.all import *

F = FiniteField(2**256 - 189)
R = PolynomialRing(F, "x")
H = lambda n: int(hashlib.sha256(n).hexdigest(), 16)

known_coefficient = H('Hero') #51862623363251592162508517414206794722184767070638202339849823866691337237984

We can then add this point to the point list given_points.append([0, known_coefficient]).

We then regenerate the list as before and obtain the correct polynomial:

91356407137791927144958613770622174607926961061379368852376771002781151613901*x^23 + 58688474918974956495962699109478986243962548972465028067725936901754910032197*x^22 + 71177914266346294875020009514904614231152252028035180341047573071890295627281*x^21 + [...] + 51862623363251592162508517414206794722184767070638202339849823866691337237984

Now that we have the polynomial, we’ll try to find their value in text, i.e. before being hashed avec sha256.

The vulnerability lay in the fact that we could calculate an extra point.

Another solution proposed by cryptanalyse is to query the server many times until we have enough points to reconstruct the polynomial.

Flag recovery

Here the vulnerability is that we have pieces of 4 characters and a small character set, so solutions are reduced.

We know that the coefficients are generated with chunks of four characters from this character set: “abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ0123456789_{}” (I’ve added the braces). This gives us a total of $ 65 ^{4} = 17850625 $ possibilities (bruteforcable).

We’ll generate a dictionary of matches value in int:plaintext and see if it matches any of the integers in our list of coefficients:

building the rainbow table 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

charset = bytes(string.ascii_letters + string.digits + '_{}')
candidate_list = list(itertools.product(charset, repeat=4))
candidate_list = ["".join(v).encode() for v in candidate_list]

rainbow_table = {}

print(f'Building the rainbow table with {len(candidate_list} entries !')

for candidate in candidate_list:
    int_hash = H(candidate)
    rainbow_table[int_hash] = candidate

# it tooks 15 seconds to build the table

assert rainbow_table[H(b'test')] == b'test'

flag_parts = [0] * len(flag_coefficients)

print("Looking up values in the rainbow table")

for coef in rainbow_table:
    if coef in flag_coefficients:
        flag_parts[flag_coefficients.index(H(b'Hero'))] = rainbow_table[coef]

Solve final

solve_interpolation.py 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

import hashlib
import re
import string
import requests
import itertools

from pwn import remote, context
from sage.all import *

host = 'crypto.heroctf.fr'
port = 9000

conn = remote(host, port)

data = conn.recvuntilS('>').decode()
given_points = eval(data.split('\n')[0])

F = FiniteField(2**256 - 189)
R = PolynomialRing(F, "x")
H = lambda n: int(hashlib.sha256(n).hexdigest(), 16)

known_coefficient = H('Hero') # 51862623363251592162508517414206794722184767070638202339849823866691337237984
given_points.append([0, known_coefficient])

interp = R.lagrange_polynomial(given_points)
flag_coefficients = interp.coefficients()


charset = bytes(string.ascii_letters + string.digits + '_{}')
candidate_list = list(itertools.product(charset, repeat=4))
candidate_list = ["".join(v).encode() for v in candidate_list]

rainbow_table = {}

print(f'Building the rainbow table with {len(candidate_list} entries !')

for candidate in candidate_list:
    int_hash = H(candidate)
    rainbow_table[int_hash] = candidate

assert rainbow_table[H(b'test')] == b'test'

flag_parts = [0] * len(flag_coefficients)

print("Looking up values in the rainbow table")

for coef in rainbow_table:
    if coef in flag_coefficients:
        flag_parts[flag_coefficients.index(H(b'Hero'))] = rainbow_table[coef]

flag = "".join(flag_parts)
print("Flag : {flag}")

It tooks 20 to 30 seconds overall.

Flag : Hero{th3r3_4r3_tw0_typ35_0f_p30pl3_1n_th15_w0rld_th053_wh0_c4n_3xtr4p0l4t3_fr0m_1nc0mpl3t3_d474}

Conclusion

The challenge was easy to understand after a quick read of the doc, it’s easy to understand where to look.

I was able to better understand Lagrange interpolation and polynomials.

Links