2024-10-30

Hacktheboo 2024 - Hybrid unifier [crypto]

Writeup for Hybrid unifier challenge at Hacktheboo 2024

Difficulty : easy

Team : crampting

Source files will be on HTB challenges platform

Author : r4sti

TL;DR

We got a server that we can contact through API endpoints.

It send us its public key.

We send it our mischievous pubic key

A session key is generated from it.

As our key is malicious, the session key is either 1 or -1.

We ask the server for a challenge which is a string encrypted with AES with the session key and we got to decrypt it and send the hash back to the server.

Then we contact the server by encrypting our request in AES and get the flag.

Introduction

The challenge is kind of a key exchange to securely generate a symmetric cryptographic key.

Then when the key exchange is done, we are supposed to interact with the server by encrypting communication with AES.

Solving

Key exchange

I didn’t save the whole source code but i will do without for the moment.

To initiate a secure session

/api/request-session-parameters
/api/init-session

After the secure session is initalized

/api/request-challenge
/api/dashboard

Creating a session initialize a Session() object with 384 bits.

sending a post request to /request-session-parameters give us the generator $g$ and the prime number $p$ :

POST /api/request-session-parameters HTTP/1.1 gives {"g":"0x2","p":"0xf4ac926dddb699f4cb03c005a9f6f89c7505ab5282a3557d2aaf41e822372edd69c2a9d4906a943340bfd87fc08f9743"}

Then we can init a session with /api/init-session in JSON by sending our public key, here is the challenge source code part:

1
2
3


def establish_session_key(self, client_public_key):
	key = pow(client_public_key, self.a, self.p)
	self.session_key = sha256(str(key).encode()).digest()

The key is generated with : $ B^{a} \mod \ p $

Where $B$ is the client public key, $a$ is the server private key.

It is how diffie-hellman key exchange is set up.

Here is a descriptive image :

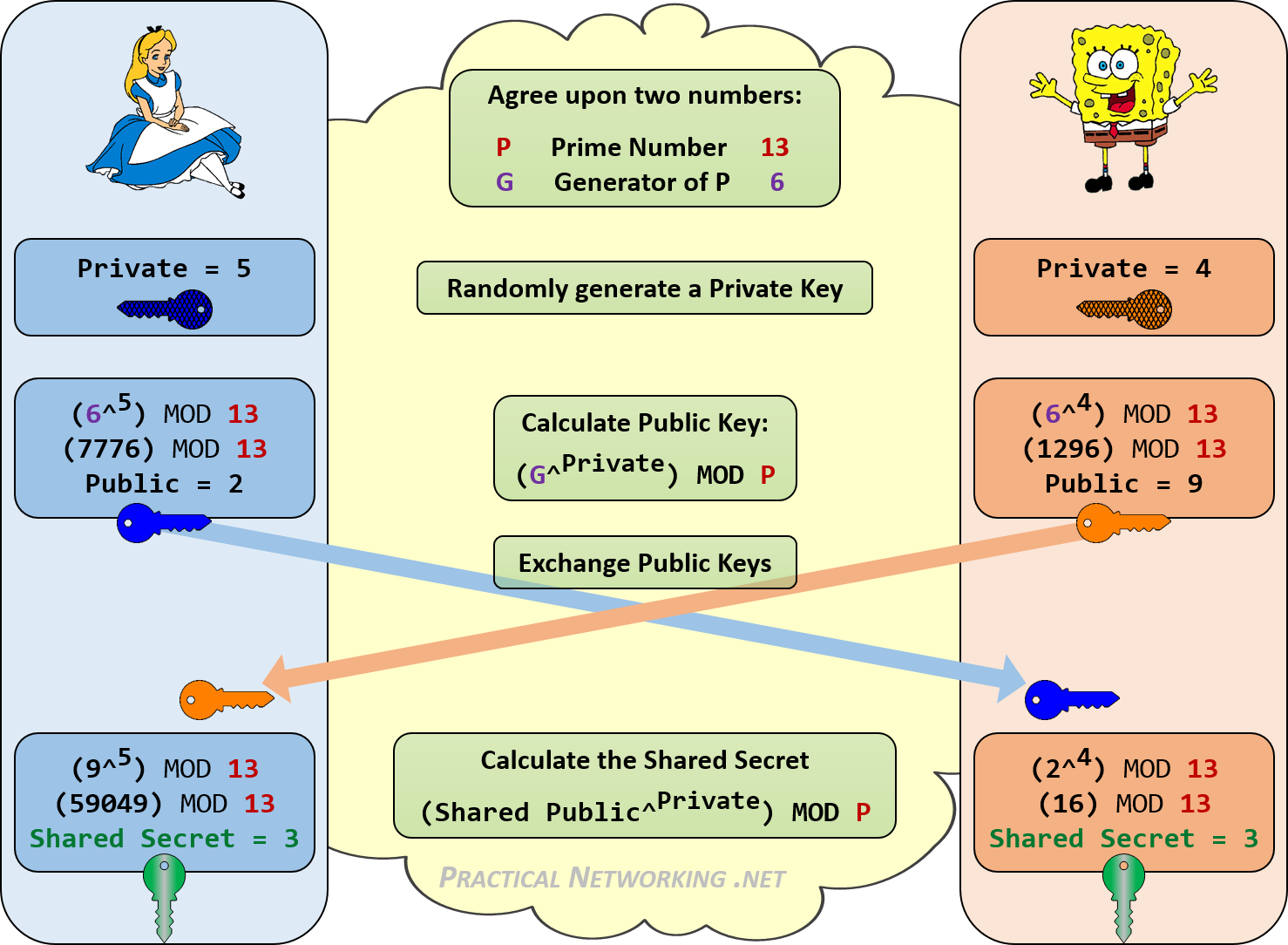
Diffie-hellman is based on modular arithmetics and thus got some interesting properties. i.e, number greater than the modulo get substracted by the modulo until they got below the modulo.

It means that with modulo p: $ p+1 = p+1-p = p $

For example :

$ a \equiv a - a \equiv 0 \mod a $

$ a + 1 \equiv 1 \mod a $

$ a - 1 \equiv -1 \mod a $

$ (a + 1) \equiv 1 \mod a $ so $ (a + 1)^{n} \equiv (1)^{n} \equiv 1 \mod p $

(There is a nice course about it on cryptohack)

So, by sending to server a public key = $ p - 1 $ or $ p + 1 $, the session key will either be -1 or 1:

With client_public_key = -1:

$$ B^{a} \equiv (p-1)^{a} \equiv (-1)^{a} \equiv -1 \ OR \ 1 \mod p $$

(it depends of the parity of $a$)

With client_public_key = 1: $$ B^{a} \equiv (p+1)^{a} \equiv 1^{a} \equiv 1 \mod p $$

For the challeng I used client_public_key = p-1 because i didn’t think to just use $1$.

The vulnerability is that the server doesn’t check the public key i send to him.

Exploiting

Now we got the key (-1 or 1), we can just use the same functions as the server to encrypt our communication (the communication is AES CBC encrypted, and then encoded with base64).

We need to contact /api/request-challenge
Decode and decrypt it
contact /api/dashboard with with a JSON with the data encrypted in AES
Get the flag

solve_hybrid_unifier.py

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83


from base64 import b64encode as be, b64decode as bd
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad, unpad
from Crypto.Util.number import getPrime, long_to_bytes as l2b
from hashlib import sha256

import requests
import json
import os

def try_decrypt(key, challenge):

    challenge = bd(challenge)
    iv = challenge[:16]
    challenge = challenge[16:]
    cipher  = AES.new(key, AES.MODE_CBC, iv)
    decrypted = unpad(cipher.decrypt(challenge),16)

    return sha256(decrypted).hexdigest()

def decrypt_packet(key, packet):
    decoded_packet = bd(packet.encode())
    iv = decoded_packet[:16]
    encrypted_packet = decoded_packet[16:]
    cipher = AES.new(key, AES.MODE_CBC, iv)
    decrypted_packet = unpad(cipher.decrypt(encrypted_packet), 16)
    packet_data = decrypted_packet.decode()

    return packet_data


if __name__ == "__main__":
    url = "http://94.237.55.180:50582"
    r = requests.post(f'{url}/api/request-session-parameters')
    data = json.loads(r.content)
    print(f"Parameters : {data}")

    g = int(data["g"], 16)
    p = int(data["p"], 16)

    my_pubkey = p-1

    # init session

    r = requests.post(f'{url}/api/init-session', json = {'client_public_key':my_pubkey})
    data = json.loads(r.content)
    print(f"Session initialization : {data}")

    server_pubkey = int(data["server_public_key"], 16)

    key_1 = sha256(str(p-1).encode()).digest()
    key_2 = sha256(str(1).encode()).digest()

    #get challenge

    r = requests.post(f'{url}/api/request-challenge')
    data = json.loads(r.content)
    print(f"Challenge : {data['encrypted_challenge']}")
    challenge = data['encrypted_challenge']
    try :
        challenge_hash = try_decrypt(key_1, challenge)
        valid_key = key_1
    except :
        challenge_hash = try_decrypt(key_2, challenge)
        valid_key = key_2

    print(f"valid key : {valid_key}")
    print(f"challenge hash found : {challenge_hash}")

    # send challenge response
    packet = b'flag'
    iv = os.urandom(16)
    cipher  = AES.new(valid_key, AES.MODE_CBC, iv)
    encrypted_packet = cipher.encrypt(pad(packet, 16))
    encrypted_packet = be(iv+encrypted_packet)

    r = requests.post(f'{url}/api/dashboard', json = {'challenge': challenge_hash, 'packet_data': encrypted_packet})

    data = json.loads(r.content)
    encrypted_flag = data['packet_data']

    flag = decrypt_packet(valid_key, encrypted_flag)
    print(f"FLAG : {flag}")

flag : HTB{good_job_in_alpha_testing_our_protocol___take_this_flag_as_a_gift_04c9f4b66afa55c164aa347e25d18148

Conclusion

It’s a nice way to understand diffie-hellman key exchange and how the choice of the key can be messed up.

Well there is another solve which was to do a classic Diffie-Hellman key exchange but my dumb ahh didn’t think about it first.